
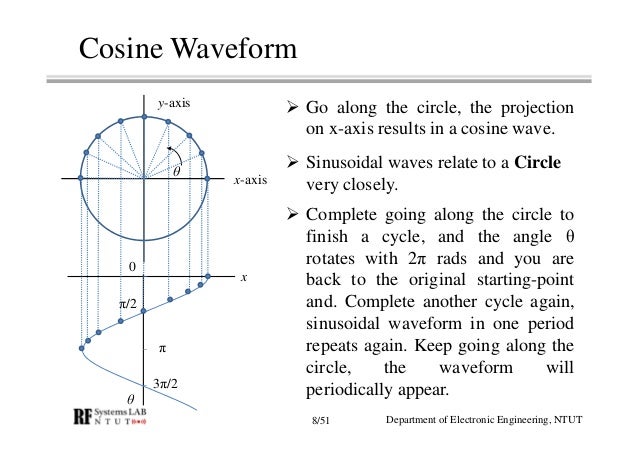
The linac may also utilize a resonator with a small RF voltage placed after the DC gun and separated from the buncher by a drift space in order to provide velocity modulation, which turns into density modulation of the beam after passing through the drift (so-called ballistic bunching). The group velocity can be numerically found as :
The beam aperture (a) defines the group velocity ( β gr) of the electromagnetic wave (collective velocity of all its spatial harmonics or energy propagation), which is related to the accelerating harmonic amplitude: smaller apertures correspond to higher accelerating field amplitudes. 3): smaller radii correspond to higher frequencies. All further discussions are valid for any harmonic chosen for acceleration, which we will call the “accelerating harmonic.”Īlthough the frequency of a DLS structure is a complex function of all dimensions, it is fair to say that it is mostly defined by the radius of the cylindrical waveguide (dimension b in Fig. Because of this fact, the beam is usually synchronized and interacts with the fundamental harmonic however, in some cases, operation on higher spatial harmonics can be beneficial due to lower phase velocities. The harmonic with m = 0 is called the “fundamental harmonic” and has the highest amplitude.
Rf toolbox phase from 0 to 2pi free#
The acceleration of a particle with charge q occurs due to the Coulomb force and interaction with the electric component E of a DC or AC field as \(\vec\), where λ is the wavelength in free space, which corresponds to the RF frequency ( f) as λ = c/f. Therefore, it is essential to understand the physics of linear accelerators and the practical design aspects of their components. Modern accelerators must satisfy the requirements for reliability, economic efficiency, and suitability for the application (such as compactness, mobility, variability, etc.), and these requirements evolve with the development of their applications. A majority of them are electron linear accelerators with moderate energies of several to several tens of MeV (see Fig. In fact, 59% of all accelerators are used for industrial and medical applications. While “big science” accelerators such as the Large Hadron Collider are the first ones to come to mind for a general reader, only ~ 1% of all accelerators are large-scale machines for research. At present, accelerators provide beams of a wide range of charged particles, from electrons to radioactive isotopes, with energies from tens of keV to multiple TeV, and currents from nA to kA.
The progress in accelerator technologies was possible thanks to advancements in beam physics, radio frequency (RF) sources, material sciences, and fabrication techniques. Particle accelerators are essential tools in nuclear and high-energy physics, medicine, material treatment, security, and industry. In this tutorial review paper, we will fill this gap with a detailed description of the bunching process and provide practical advice on the design of bunching sections in industrial-grade electron linacs. The physics of non-relativistic motion is described in the literature on ion accelerators, but in practice, it cannot be scaled to electron machines due to the significantly different particle mass and acceleration rate, beam velocity change, and frequencies. Although many books describe the theoretical and practical aspects of electron linac design, most of them concentrate on beam physics in either the gun stage or in the relativistic regime, while leaving the description of the bunching process rather general. The acceleration of electrons in resonant linear accelerators (linacs) typically consists of three main stages: (1) emission of the electrons from the cathode and their pre-acceleration with a DC field to the energy of tens of keV (2) grouping the DC electron beam into bunches and their synchronization with the correct phase of high-frequency electromagnetic fields, and (3) accelerating the bunches of relativistic electrons to the required energies.


 0 kommentar(er)
0 kommentar(er)
